Copycat is a new project for which I will copy parts, or maybe even everything, from a program. Just to see if I can manage to get the exact same part done. Of course I will write about it how I did it. Call it a learning experience.
Take for example the utility Ranger from Steven Solie. Have a look at the Machine tab from that utility. Would it not be great to know how to get that kind of info? For my first project I will do exactly that. Create a copy of the machine tab from Ranger. First I will just print out all the info and once I have that done I will even create the same look. It will teach me how to get that machine info and also how to create such a layout. It will be a lot of fun.
I knew I had not done anything on the File Manager for some time but that the last post was almost a year ago even surprised me. That is probably also the last time I did any programming on it. I even had to read back to see what I was up to at that moment. I decided to continue on Aros using Zune which is an object-oriented GUI toolkit. It is nearly a clone (at both API and Look&Feel level) of MUI, a well-known Amiga shareware product by Stefan Stuntz. I am going to switch back to OS4.1 using ReAction. At the time I was still programming using ReAction the wrong way. Since I am doing it the correct way with my Redhouse Editor project I decided to ditch all the current code and use the Redhouse Editor code for which I program ReAction the correct way. So what I have at the moment is a window that is being opened and already has a small menu system in place.
The above Window is what I have at the moment. Simple but proper ReAction code so a good start if you ask me. What I plant to do next is to play around a bit with the layout. Getting myself a bit familiar with the Layout Class to make it look like a bit more like a File Manager. When you talk about a File Manager look you instantly think about the two column look like you can see below from Directory Opus.
For this I will have to use the List Browser Class. I remember how difficult it was last time I tried to have a go at it. I better be prepared this time and get the job done.
The errors I reported in my previous column did not go away. I ended up formatting the DH2 partition using SFS/02 to see how that will work. It has the same problem as JXF that there are no recovery/fixing tools once something goes bad. Seeing as it only happened once with JXF I don’t worry much about it. Programs can be re-installed and with regular backups moved to a different storage device I should be pretty safe.
I posted about it on AmigaWorld which caused a massive amount of replies and discussions.
I thought I would play Shadow of the Beast on my A1200. I used Multi Kickstart to get Kickstart 1.3 running and start the game. It look promising since it runs smooth till the title screen. But once you start to play the game it looks all messed up and when you start playing it crashes. I really need to get a TV modulator for my A500 so I can play those classics. Most classic games won’t run on my A1200 even with a degrader like Multi Kickstart. Or I need to get another monitor so I can use my A500 again. I probably look into this later this year since I am sure I can pick on up cheap at one of the Amiga meetings / gatherings.
But why not try the A600HD I have? That always had a better ratio of working classic games. It is just sitting in the box anyway. I tried Shadow of the Beast which failed on the A1200HD and it works perfectly. So it was that easy? Oh no, not at all. There are always issues. Turns out I had picture but no sound. I even tried two televisions set. The plus from that was that the other one I tried had a better picture. After posting on AmigaWorld it was suggested to use a composite connection. It took me a bit to find out that I need to set the television set to AV to get it to work. Better picture and sound. Of course there was another problem. The sound is not correct. It is not playing all the sounds like it suppose to do. Come to think of it I remember having this issue before with my A600HD and 1084 monitor. So being a hardware issue there is nothing I can do. I did see a cable on AmigaKit that can be used to get get the video and sound from my A500 to the television set. Maybe I order such a cable in the future when I order something from them again. Who knows I might even pickup a cheap monitor before that. At least I have a better picture with my A1200HD on my television set now.
Due to this two issues I spent a lot of time on AmigaWorld this week. It has been a long time that I spent some time on there. Usually it is just for a quick look for news. This coming week I want to spent some time on my programming. I will focus on the Redhouse File Manager so I can get some more programming done on it. At the same time I will write about it. I will also post something about the Redhouse Editor. It sure is going to be a busy week when it comes to the Amiga. Just how I like to see it.
My A1200HD is up and running again after being “retired” for a bit due to lack of space. I created some space and sourced a table so I could set it up again. I am using a TV since my monitor died on my some time ago. I just love the look and feel when playing Amiga games on the TV. Everything still works as it should. Due to only 2 MB of memory I use the CLI to transfer files from my laptop to my Amiga. This works really great. I have two memory cards which allows me to use a GUI FTP (like AmitFTP) to transfer files but for some reason they give my A1200HD issues. It works fine for a while but suddenly it switches off and will not turn on again. The power light keeps flashing. If I wait a bit it will work again and sometimes it keeps doing it again right away but also works for a longer time but eventually the problem surfaces again. But I am at peace with the CLI using NCFTP to transfer files.
I am sure I talked about it before about me having lost my degrader disk. I use this to get Kickstart 1.3 loaded on my A600 or A1200 so I can play games that won’t run on the new Kickstart.
I remember looking for it everywhere and as always it turns up when you don’t expect it. It is called Multi Kickstart and it was written by SinSoft.
It does not work for every game of course as many of you might have experienced.
There is a new update of AmiUpdate. Version 2.34 is out which I installed right away of course. AmiUpdate is the first utility I run when I have booted up OS4.x.
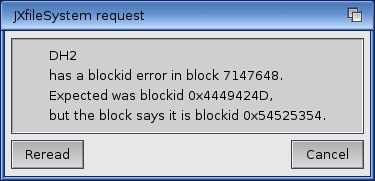
Out of nowhere I suddenly start getting these JXfileSystem errors popping up. I remember seeing something on the screen when I started OS4.1 but everything seemed fine once it was up and running. But I should have known better. It does seem to be related to my DH2 drive which contains my applications. I already posted about this on AmigaWorld to see what can be done but I fear a format of the partition is the only way. Maybe it even will go away and I can go back to normal like this never happened. Fingers crossed!
Summer finally arrived and boy is it hot. It goes from bearable to extreme making “computing” less fun. Today is one of the “cold” days so time to get something on “paper”. Besides this I will get some programming work done and play some classic Amiga games with hopefully a bit of time to write a review.
Something I did try in the last couple of time was Qt 4.7. It was a real struggle to get it installed. The biggest problem was to get in on to my Amiga. I tried to download it first but OWB froze all the time not capable of getting the full file which was 400+ MB in size. NetSurf did get it in one time but the file was corrupt. Tried it twice if I remember correctly but both times I ended up with a corrupt file. Next up was a FTP transfer and I tried it with the Amiga as a server and my laptop with Windows 8 as a server bot no matter which setup it did not work. Either it froze every time after a few seconds or it kept going for a bit longer till it also froze. With the resume option I could continue and with one setup I did manage to get to the 400+ MB size but it kept going and going reaching over 500+ MB which meant this was not going to work. Next up was DVD transfer and even with two rewrite-able’s I still got a corrupt file error. After doing a bit of searching I came across FTPMount which allowed me to transfer the whole file without ending up being corrupt. What a great tool this is. I use it with the CLI (old school style) and I was really impressed. I will try it a bit more transferring large files to see if it was not a lucky moment I had with Qt.
So how is Qt4.7? I don’t like one bit. I expected this already but it is a resource hungry program. So most Qt programs will not run. The ones that do are sluggish and they look messed up. It is hard to explain but it is like you see two windows. It is like the programs window is displayed in a OS4.x window so you see the outer parts of the OS4.x window around the Qt window. Of course I only use 128 MB of memory so I should not expect a lot. At least I had a try and I got to know FTPMount so it was not completely fruitless.
There is one topic I am really interested in and that is having a Basic programming language on OS4.x. I grew up with Amos and I always have had a love for Basic like languages. There have been attempts to get a Basic language on to the OS4.x platform while also targeting other platforms at the same time. None of them never really amounted to anything. We can debate if such a language is really needed let alone the time that is needed to get it done. There is Hollywood, the easy to use “program language” so in a away that area is covered for OS4.x. I never used Hollywood myself so I can’t make any comments on it at all. But wouldn’t it be great if there was a Amos like Basic language on OS4.x? A simple way of programming difficult programs, games, demos etc. while still learning the art of programming? No drag and drop but writing the code yourself yet shielding you from the bits that would make you normally scream and run away. I guess that would be really cool.
What are the chances of something like this ever to appear on OS4.x? About zero I would say. I thought about it often if I should not have a try myself. I know more about cars than about creating a Basic program language and I don’t know anything about cars. None the less I have decided to dive into this to see what I am capable of and how far I would get. This is really a starting from scratch, or struggling if you like, project with epic fail written all over it. I will be writing about it in detail so you all get to learn something. If it fails I at least give it a try instead of only thinking about it without actually doing anything. Here’s to the mess I probably will get myself into.
The one thing from this disk that I remember vividly is the Flood demo. Throwing those hand grenades was the coolest thing you could do.
I should have the disk somewhere but it would not surprise me if I used it for another game or program. Disks did not come cheap so whatever you did not really need you used to copy something else on. I still try to remember if I have the magazine. It must be somewhere together with all the other magazines.
You can download the coverdisk from Amiga Magazine Rack.
I played the Flood demo a lot. I remember that at one point all I did was throw those grenades. But Flood is a good platformer and certainly something you would play again. The great thing about these demos is that you get a good feel of the game before you part with your cash.
The Plague is not really my kind of game. I played the demo a couple of times and I even might have played the full version a couple of times. CU Amiga did gave it the highest rating of the ones I could find. Mark Winstanley from Amiga Power describes it as… “The Plague? I’d rather have tetanus”.
Who didn’t use Soundtracker? It is part of the Amiga history books as so many other great things. Soundtracker is guaranteed to give you hours if not days of material to talk about.
I still have my Soundtracker disks. Once I have my A1200 setup again I will see if they still work. I am pretty sure I had different versions over time. Floppy disks did not come cheap and sometimes you needed some for new games, demos or programs so you used disks containing stuff you would not use for some time anyway. Of course you regretted it not long after it.
There was one module you wanted to try first before any other ones. Which one? AxelF of course! Time to look for some other great classics.
Good old fun. That’s how I would describe Mikey Does the 80’s Again!!! (Take 2) show from Thursday 27-6-2013.
I had a great time and it was a real blast from the past. I talked about it before but when we still lived in Thailand I listened to Mikey’s show a lot. So this one brought back some really great memories. I hope he does another one (Christmas?) and for sure I will be tuning in.
Commando is a game that just won’t work with WinUAE. I had not upgraded to the latest version for some time but today I thought I would do so and while doing this I thought it might be a good idea to try Commando again. And what a surprise it was that it worked. So far I just tried the first bit of the game so it could be it fails later on in the game. This type of game is really my favorite. Sadly the C64 had more of these type games compared to the Amiga. I use the word sadly not to offend the C64 but for the fact I had no C64.
So far I posted two articles that contained video(s). One was about Licence to Kill and the other about Run the Gauntlet. I will use it more often as it gives the articles that extra touch of greatness. I am already working on a new article which will include a video that will just give it that extra bit. You will see.
Trevor posted a new article on his blog in which he talks about the Silicon Dreams/VCF 2013 (UK tech show) taking place on 5-7 July 2013. They hope to show a few interesting things but no promises. I will keep an eye on the this next weekend and hopefully we do get to hear about some interesting things.
I did a review on Run the Gauntlet some time ago. I did gave it a rather bad score. I am still sticking to it even after I played it again for this section. I actually started to dislike it even more. The horrible controls for the game are just killing it. I actually had some fond memories about the game but it must have been the show on the telly. Also in most cases the fond memories are more about what was happening at the time of playing the game. That usually makes you think it was a great game until you actually start playing it again. Don’t get me wrong, not all games with great memories turn out to be bad.
The best thing about the game for me is the intro. “Hi, I’m Martin Shaw. This is Run The Gauntlet. If you want to see Action Sports…. This is the place to be!” It’s worth it just to fire up the game for the intro. I remember doing that a lot with the speakers on full.
Most memorable gaming moments does not necessarily mean good things. One thing I always hated, and happened near the finish just about outrunning the competitors, is when the explosion happened right when you are going over it with your speedboat, hovercraft or jet ski. Let me know if you have any Run the Gauntlet memorable gaming moments.
If you read my Licence to Kill review you know about me trying to get to the next level in Scene 2 part 1 and that I was stuck. But thanks to the movie I was able to figure out what to do. For me this is a memorable gaming moment.
As you can see from the video you need to “harpoon” the plane. At first I thought you have to stay behind it for a certain time to finish the level. But trying to do that for some time without nothing happening got me thinking that this was not the way to go. In the movie 007 climbs aboard the plain so that made me think I need to get to the plane. After trying the controls I figured out to movie to the plane, climb aboard and complete the level. That was a great feeling to be able to finish that level. Especially since I was stuck here for a long time.